Czy Archimedes miał parcie?

Kto z nas nie słyszał słynnej legendy o Archimedesie i problemie jaki dostał do rozwiązania od Hierona II króla Syrakuzy? Grek miał wykrzyknąć słynne Eureka i wybiec radośnie z kąpieli. Zaobserwował on, że ciało wrzucone do wody wypiera pewną jej części, a obserwacja ta była kluczem do odpowiedzi na pytanie czy królewska korona wykonana jest ze złota. Archimedes wykonał dwie bryły o ciężarze korony – jedną ze złota i jedną ze srebra. Okazało się, że złota próbka wyparła mniej wody niż srebrna (złoto jest bardziej gęste, a więc przy tej samej masie miało mniejszą objętość). Gdy uczony porównał wyniki z objętością wody jaką wypchnęła korona okazało się, że wypchnęła więcej wody niż czyste złoto. W ten sposób Archimedes udowodnił, że król został oszukany oraz odkrył prawo będące kluczem do wytłumaczenia dlaczego statki pływają.

Czy Archimedes miał parcie?

Parcie? Każdy student mechaniki i budowy maszyn nie kojarzy dobrze tego słowa. Parcie to inaczej siła z jaką woda lub inne płyny naciskają na różne obiekty. Zależy ona oczywiście od tego jak wielki jest obiekt, jaki ma kształt oraz jak głęboko jest zanurzony (ciśnienie rośnie wraz z głębokości – przynajmniej w polu grawitacyjnym). Co to ma wspólnego z prawem Archimedesa? Bardzo wiele bo to tak naprawdę jedno i to samo – przynajmniej moim zdaniem, a to jedno z moich ulubionych praw.

Pomyślmy sobie o parciu, które powodowane jest przez ciśnienie hydrostatyczne. Widzimy je patrząc jak rozpychane są ścianki butelki pod wpływem jej napełniania. Możemy zaobserwować jego zmianę gdy wykonamy w butelce otwory na różnej wysokości i będziemy obserwować jak daleko tryskają z nich strumienie wody (w zasadzie strugi, ale strumień to przyjaźniejsze i mniej techniczne słowo). Ba! Poczujemy je w postaci bólu uszu gdy zanurkujemy głęboko w wodzie. Jednak co ma to wspólnego z prawem Archimedesa? Wszystko.

Przeprowadźmy myślowy eksperyment i wyobraźmy sobie kulkę zanurzoną w wodzie. Ciśnienie naciska na każdy jej skrawek. Możemy jednak sobie łatwo wyobrazić, że tak naprawdę jest ona naciskana przez cztery siły. Jak na rysunku. Jednak górna czasza kuli dociskana jest do dołu, a dolna ku górze. Czerwone i niebieskie linie reprezentują ciśnienia jakie działają na naszą kule. Co jeśli je odejmiemy? Zakreskowana zostanie jedynie objętość kuli! Eureka!

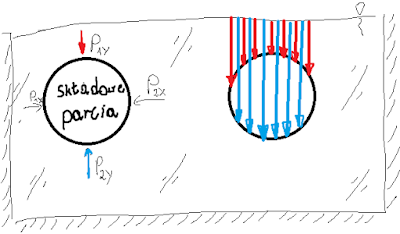Rysunek 1. Siły działające na ciało
(właśnie dlatego nie jestem grafikiem, ani malażem)

Ponieważ pozostało jedynie niebieskie pole to jest to odpowiednik siły, która wypych ciało na wierzch. Oczywiście zapełnia ono całą objętość kuli/lub innego ciała i jest to właśnie siła jaka zadziała na nasz obiekt zanurzony. Tak o to parcie zamienia się w prawo Archimedesa, a dla żądnych wyjaśnień na końcu wzory.

Gdzie jednak stosujemy parcie i prawo Archimedesa? Oczywiście wszędzie tam gdzie coś pływa – łodzie podwodne, kadłuby statków – oraz tam gdzie może polecieć – Zeppeliny, balony. Istnieje również nurek Kartezjański. Urządzenie można wykonać z butelki w której zanurzamy balonik, słomkę albo plastikową skuwkę (po tylu latach edukacji w końcu użyłem tego słowa) obciążoną plasteliną. Ściskając butelkę powietrze w nurku zmniejsza objętość co powoduje zmniejszenie siły wyporu i zatapianie nurka. Jest to dość prosty ale naprawdę fajny eksperyment pokazujący prawo Pascala (mówiące o tym, że gazy są bardziej ściśliwe od cieczy).

Czy Wy macie jakieś ulubione prawa? Niekoniecznie związane z mechaniką płynów?

Prawo Archimedesa obliczone z parcia

PS. Można to oczywiście wliczyć z twierdzenia Ostrogradskiego-Gaussa o czym informuje nas Wikipedia. Jednak przeciętny student do nie zna i nie pozna, a parcie poznało naprawdę wiele osób. Dowodzik jest prosty i mimo, że nie jest to dowód w matematycznym rozumieniu tego słowa to mi sprawia radochę.

Źródła i ciekawe linki:

1.Elżbieta i Janusz Kubrak, Podstawy obliczeń mechaniki płynów w inżynierii i ochronie środowiska, Wydawnictwo SGGW, Warszawa 2010.

2.Pływanie ciał, prawo Archimedesa i trójkąt bermudzki!, Fizyka od podstaw, YouTube

3.Wiki